Correlation

Validation

0.1.0

Here we compare the results of PAMLj with other software that performs power analysis. In particular, we will compare our results with R pwr package and G*Power.

For Pearson and Spearman correlation, we can compare PAMLj with R pwr package and G*Power. Consider, however, that for this task PAMLj employs R pwr package under the hood, so the results are obviously in line. For G*Power, the comparison represents a proper validation. All packages use the inverse hyperbolic tangent transformation (Cohen 1988).

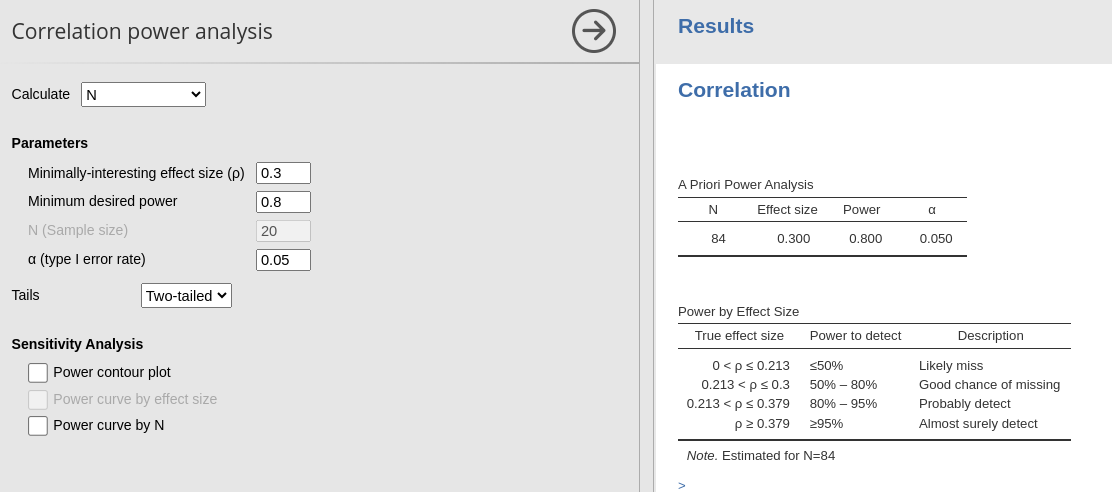
Example 1 : Sample size

Setup

  • Aim = Sample size
  • Expected r = .3
  • Required power = .8
  • Alpha = .05

PAMLj

R

pwr::pwr.r.test(r=.3,power=.8,sig.level=.05)
## 
##      approximate correlation power calculation (arctangh transformation) 
## 
##               n = 84.07364
##               r = 0.3
##       sig.level = 0.05
##           power = 0.8
##     alternative = two.sided

G*Power

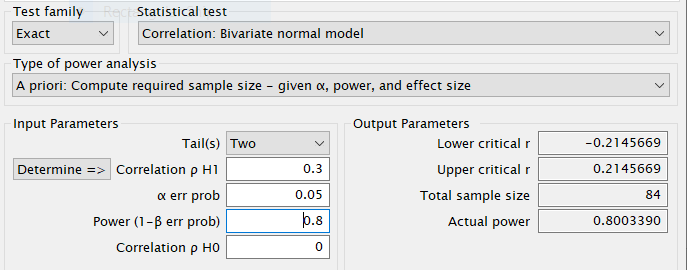
If we round the results, they are the same

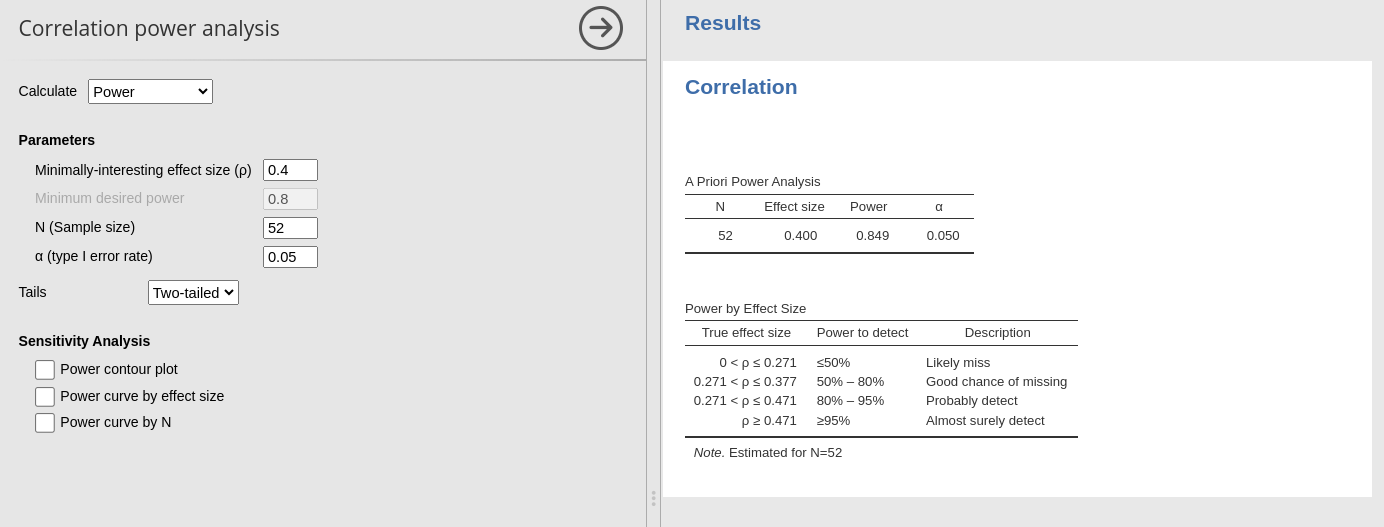
Example 2: Power

Setup

  • Aim = power
  • Expected r = .4
  • N = 52
  • Alpha = .05

PAMLj

R

pwr::pwr.r.test(r=.4,n=52,sig.level=.05)
## 
##      approximate correlation power calculation (arctangh transformation) 
## 
##               n = 52
##               r = 0.4
##       sig.level = 0.05
##           power = 0.8485972
##     alternative = two.sided

G*Power

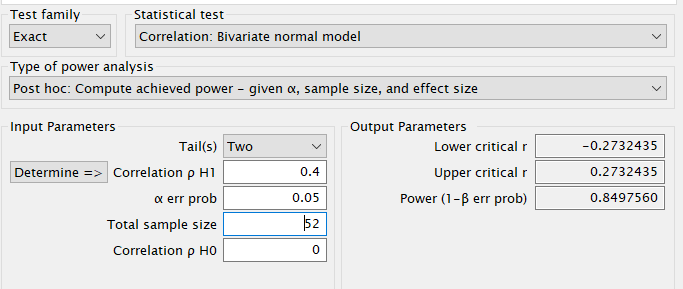
Results are the same at the third decimal place, which can be consider quite good.

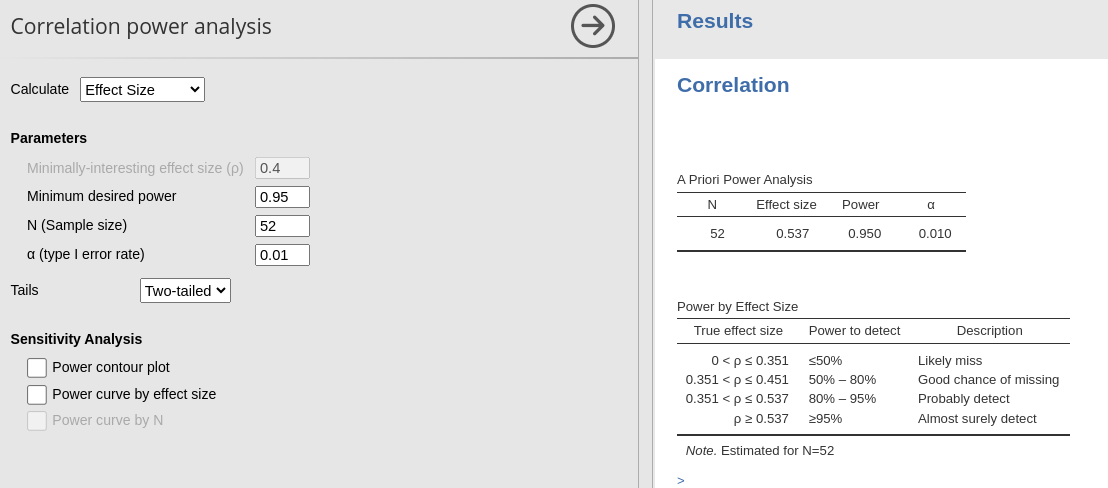
Example 3: Effect size

Setup

  • Aim = minimal effect size
  • power = .95
  • N = 52
  • Alpha = .01

PAMLj

R

pwr::pwr.r.test(n=52,power=.95,sig.level=.01)
## 
##      approximate correlation power calculation (arctangh transformation) 
## 
##               n = 52
##               r = 0.5369775
##       sig.level = 0.01
##           power = 0.95
##     alternative = two.sided

G*Power

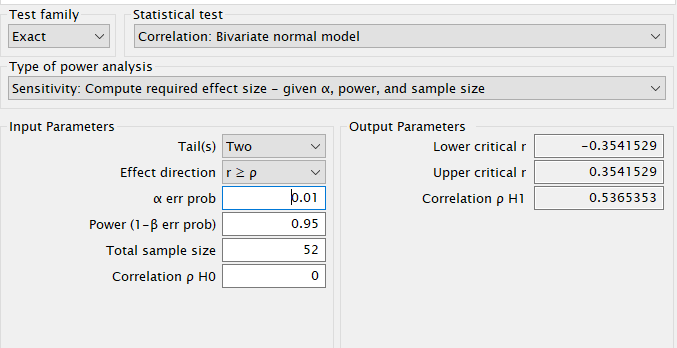
Again, rounding a the third decimal place, results are the same.

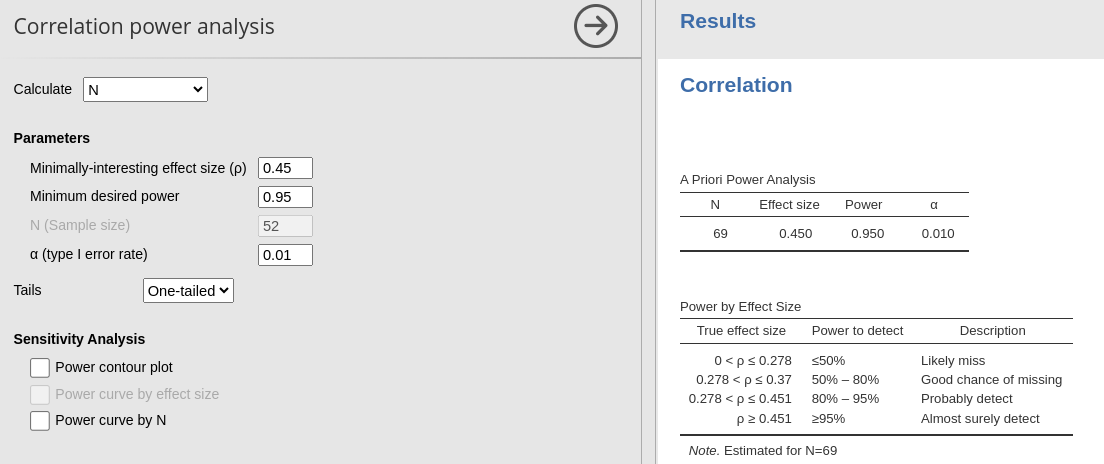
Example 4: One-tail

Setup

  • Aim = Sample size
  • power = .95
  • Expected r = .45
  • Alpha = .01
  • Tails = “one.sided”

PAMLj

R

pwr::pwr.r.test(r=.45,power=.95,sig.level=.01,alternative="greater")
## 
##      approximate correlation power calculation (arctangh transformation) 
## 
##               n = 69.45436
##               r = 0.45
##       sig.level = 0.01
##           power = 0.95
##     alternative = greater

G*power

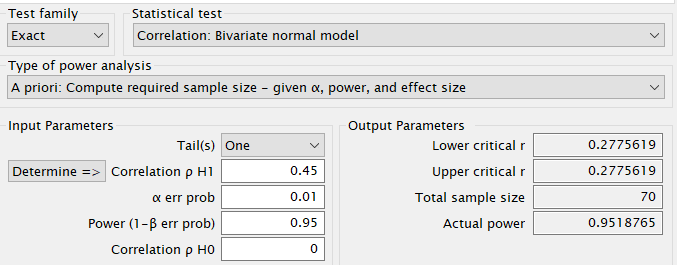
In this case, notice that PAMLj yield 69, which is rounded for 69.45, whereas G*Power round it up to 70. Thus, results are quite in line.

Comments?

Got comments, issues or spotted a bug? Please open an issue on PAMLj at github or send me an email

Back to

PAMLj: rosetta, PAMLj

References

Cohen, J. 1988. Statistical Power Analysis for the Behavioral Sciences. Lawrence Erlbaum Associates.