Independent sample T-test: Equivalence tests

Power Analysis

0.2.0

Here we compare the results of PAMLj with published results and other software that performs equivalence tests for the t-test.

Independent sample t-test

For the independent samples t-test, we will refer to Lakens (2017) Table 1 , in which sample sizes are reported for an equivalence test with expected value \(\delta=0\) and varying “Bound”, in PAMLj refereed to as equivalence limit . Lakens (2017) Table 1 reports results for \(\alpha=.05\) and \(\alpha=.01\). The table (available here) is reproduced below.

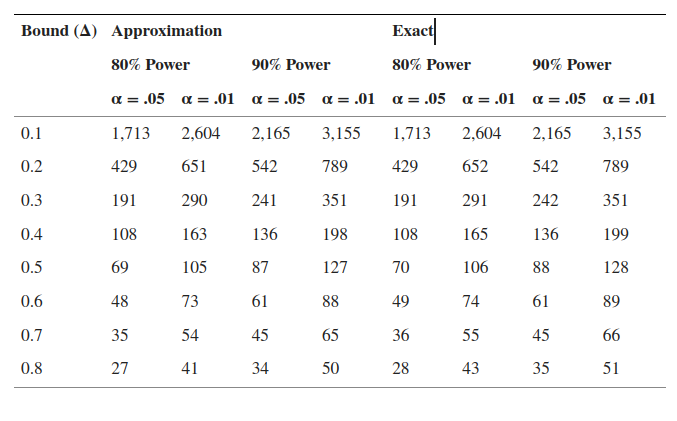
The table reports the required N (per group) to obtain a sufficient power (80% or 90%) given a certain \(\alpha\) and a certain limit \(\Delta\) of equivalence.

To compare the results with R, we are going to use results from powerandsamplesize.com website, in which the R code of their nice online calculator is public and open, so we could implemented in R to make comparisons.

PAMLj

For the firs test, we insert an Equivalence limit of \(.1\), an expected \(\Delta_d=0\), power=.80 and \(\alpha=.05\).

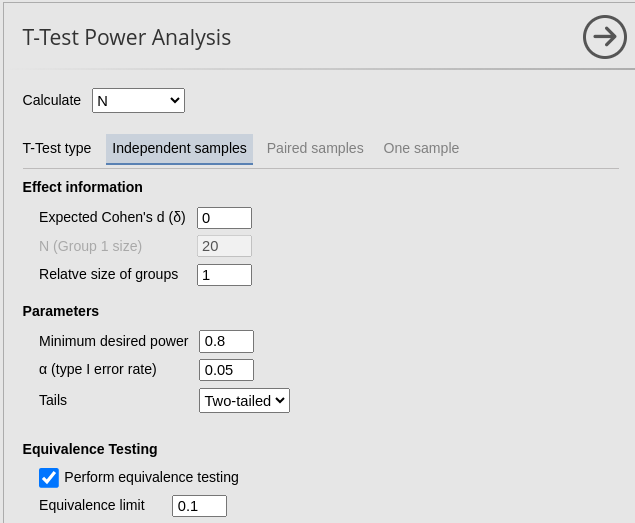
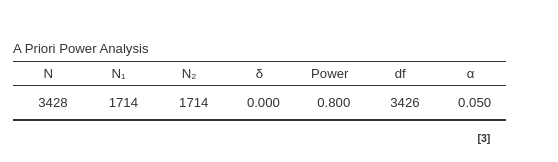
As expected, the results are quite similar. The 1-unit difference observed (1714 vs 1713) is simply due to the rounding, which may yield slightly different results across different software.

R

muA=5
muB=5
delta=1
kappa=1
sd=10
alpha=0.05
beta=0.20
nB=(1+1/kappa)*(sd*(qnorm(1-alpha)+qnorm(1-beta/2))/(abs(muA-muB)-delta))^2
z=(abs(muA-muB)-delta)/(sd*sqrt((1+1/kappa)/nB))
ceiling(nB)

## [1] 1713

(Power=2*(pnorm(z-qnorm(1-alpha))+pnorm(-z-qnorm(1-alpha)))-1)

## [1] 0.8000048

For \(\Delta_d=.2\) we proceed as before.

PAMLj

For the firs test, we insert an Equivalence limit of \(.1\), an expected \(\Delta_d=0\), power=.80 and \(\alpha=.05\).

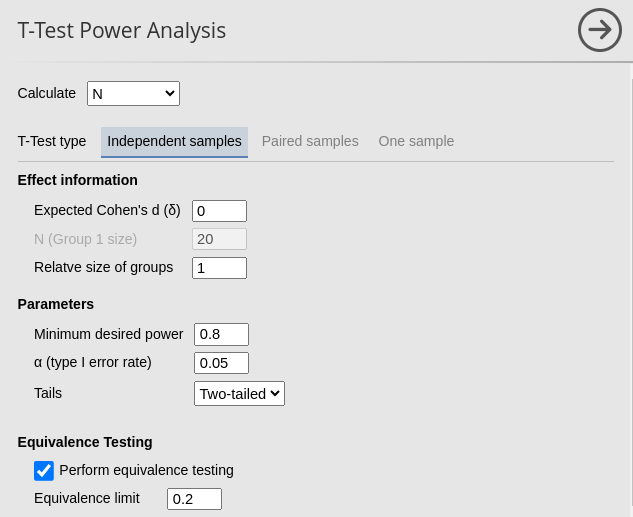
R

muA=5
muB=5
delta=2
kappa=1
sd=10
alpha=0.05
beta=0.20
nB=(1+1/kappa)*(sd*(qnorm(1-alpha)+qnorm(1-beta/2))/(abs(muA-muB)-delta))^2
z=(abs(muA-muB)-delta)/(sd*sqrt((1+1/kappa)/nB))
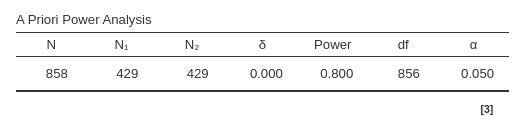
ceiling(nB) # 108

## [1] 429

(Power=2*(pnorm(z-qnorm(1-alpha))+pnorm(-z-qnorm(1-alpha)))-1)

## [1] 0.8000048

Again, results are identical even after rounding.

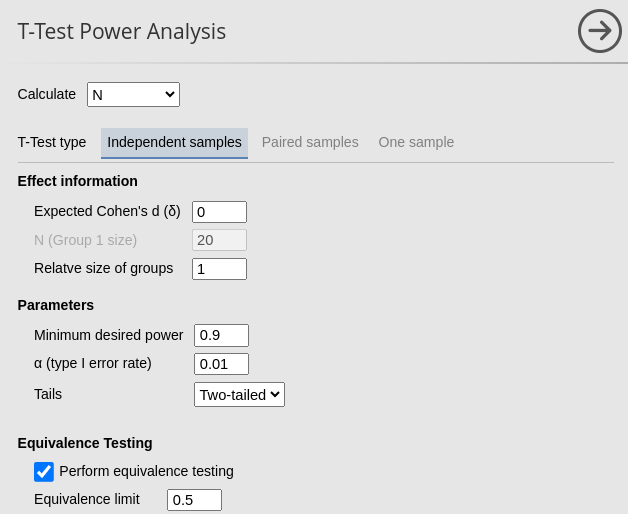
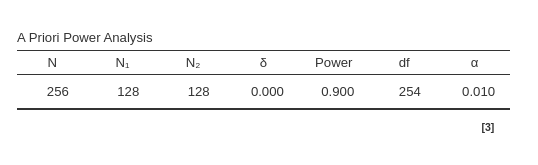
As a final test, we try \(\Delta_d=.5\), \(\alpha=.01\), power=.90, expecting \(N=128\) (see table under “exact” columns).

PAMLj

For the firs test, we insert an Equivalence limit of \(.5\), an expected \(\delta=0\), power=.80 and \(\alpha=.05\).

R

muA=5
muB=5
delta=5
kappa=1
sd=10
(d <- (muA-muB)/sd)

## [1] 0

(delta_d <- (delta)/sd )

## [1] 0.5

alpha=0.01
beta=0.10
nB=(1+1/kappa)*(sd*(qnorm(1-alpha)+qnorm(1-beta/2))/(abs(muA-muB)-delta))^2
z=(abs(muA-muB)-delta)/(sd*sqrt((1+1/kappa)/nB))
ceiling(nB) # 108

## [1] 127

(Power=2*(pnorm(z-qnorm(1-alpha))+pnorm(-z-qnorm(1-alpha)))-1)

## [1] 0.9

Paired t-test

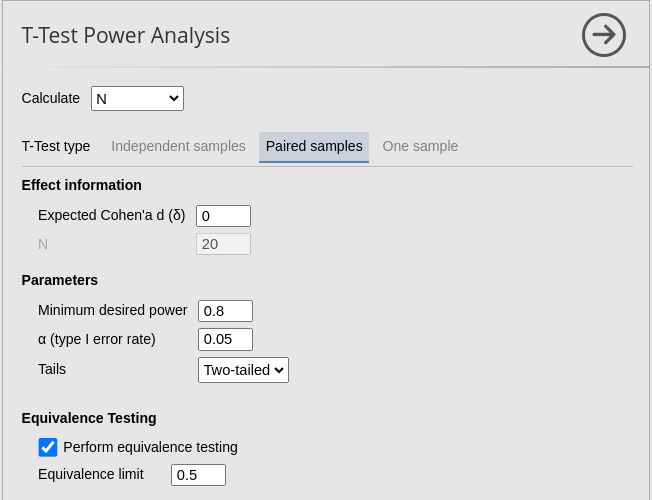
To compare the results with R, we are going to use results from powerandsamplesize.com website. The code is for comparing one mean with a population value, which is equivalent to compare the difference between two means in a paired sample (repeated measures).

In the first example, we have As a final test, we try \(\Delta_d=.5\), \(\alpha=.01\), power=.90, expecting \(N=128\) (see table under “exact” columns).

R

mu=2
mu0=2
delta=0.05
sd=0.10
(d<-(mu-mu0)/sd)

## [1] 0

(delta_d<-(delta)/sd)

## [1] 0.5

alpha=0.05
beta=0.20
(n=(sd*(qnorm(1-alpha)+qnorm(1-beta/2))/(delta-abs(mu-mu0)))^2)

## [1] 34.25539

ceiling(n) # 35

## [1] 35

z=(abs(mu-mu0)-delta)/sd*sqrt(n)
(Power=2*(pnorm(z-qnorm(1-alpha))+pnorm(-z-qnorm(1-alpha)))-1)

## [1] 0.8000048

PAMLj

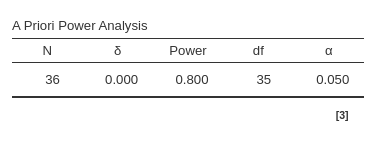
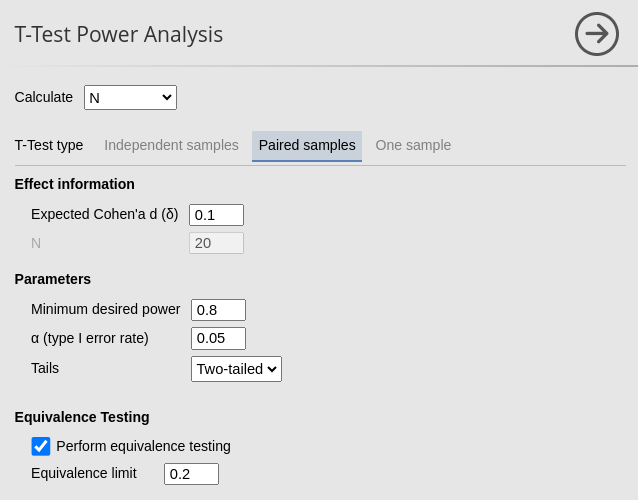
Now, we test an equivalence test assuming that the expected value is not exactly one.

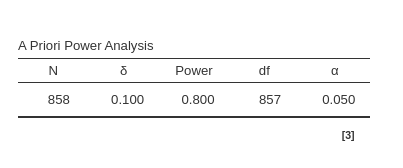
R

mu=3
mu0=2
delta=2
sd=10
(d<-(mu-mu0)/sd)

## [1] 0.1

(delta_d<-(delta)/sd)

## [1] 0.2

alpha=0.05
beta=0.20
(n=(sd*(qnorm(1-alpha)+qnorm(1-beta/2))/(delta-abs(mu-mu0)))^2)

## [1] 856.3847

ceiling(n) # 35

## [1] 857

z=(abs(mu-mu0)-delta)/sd*sqrt(n)
(Power=2*(pnorm(z-qnorm(1-alpha))+pnorm(-z-qnorm(1-alpha)))-1)

## [1] 0.8000048

PAMLj

Comments?

Got comments, issues or spotted a bug? Please open an issue on PAMLj at github or send me an email

Back to

PAMLj: rosetta, PAMLj

References

’

Lakens, Daniël. 2017. “Equivalence Tests: A Practical Primer for t Tests, Correlations, and Meta-Analyses.” Social Psychological and Personality Science 8 (4): 355–62.